fluida dinamis
tugas proyek fisika kelas XI semester ganjil
guru indri dayana,M.Si
materi pembelajaran:fluida dinamis
tujuan pembelajaran:mengetahui konsep fluida iddeal,garis arus dan asas kontinuitas,asas bernoulli dan mengetahui pnerapan penerapan asas kontinuitas dan asas bernoulli dalam kehidupan serta dapat mengerjakan latihan latiahn fluida dinami
apakah yang dimaksud dengan fluida dinamis? fluida dinamis adalah fluida yang bergerak.
beberapa konsep tentang fluida dinamis:
1.fluida termampatkan :fluida yang volume atau massa jenisnya berubah ketika diberi tekanan
2.fluida tak termampatkan :fluida yang volume atau massa jenisnya tetap ketika diberi tekanan
3.aliran tunak : aliran fluida dimana kecepatan fluida di setiap titik adalah tetap.
4.aliran tidak tunak: aliran fluida dimana kecepatan fluida di setiap titik tidak tetap
5.aliran berputar: fluida tersebut mengalami momentum sudut terhadap suatu titik tertentu
6. aliran tidak berputar: fluida tersebut tidak mengalami momentum sudut terhadap suatu titik tertentu
7. fluida kental: fluida dimana gesekan internal di dalam fluida tidak dapat diabaikan sehingga benda bergerak melalui fluida tersebut mengalami gaya gesekan
8.fluida tak kental :fluida dimana gesekan internal di dalam fluida dapat diabaikan sehingga benda bergerak melalui fluida tersebut tidakmengalami gaya gesekan
garis arus dan asas kontinuitas
1. garis arus
adalah lintasan yang ditempuh oleh partikel-partikel fluida yang mengalir dengan aliran tunak.
2.asas kontinuitas
sebelum mempelajari asas kontinuitas terlebih dahulu memahami konsep debit
debit adalah besaran fisis yang menyatakan volume fluida yang mengalir melalui suatu penampang tiap satuan waktu.
jd persamaan kontinuitas adalah Persamaan kontinuitas adalah persamaan yang menghubungkan kecepatan fluida dalam dari satu tempat ke tempat lain
menurut asas kontinuitas "untuk fluida tak termampatkan hasil kali antara luas penampang dengan besar kecepatan fluida selalu tetap" karena hasil kali antara luas penampang dengan kecepatan adalah debit aliran fluida maka pernyataan lain dari asas kontinuitas adalah "untuk fluida tak termampatkan,debit aliran fluida di setiap titik adalah tetap."
contoh soal:
Pipa saluran air bawah tanah memiliki bentuk seperti gambar berikut!

Jika luas penampang pipa besar adalah 5 m2 , luas penampang pipa kecil adalah 2 m2 dan kecepatan aliran air pada pipa besar adalah 15 m/s, tentukan kecepatan air saat mengalir pada pipa kecil!
Pembahasan
Persamaan kontinuitas
A1v1 = A2v2
(5)(15) = (2) v2
v2 = 37,5 m/s
C. asas bernouli
Hukum Bernoulli adalah hukum yang berlandaskan pada hukum kekekalan energi yang dialami oleh aliran fluida. Hukum ini menyatakan bahwa jumlah tekanan

persamaan ini mempunyai makna fifis yaitu "untuk fluida ideal yang mengalir melalui suatu penampang,jumlah tekanan,energi potensial per satuan dari fluida tersebut di setiap titik sepanjang garis arus bernilai konstan"
D.penerapan asas kontinuitas dan asas bernoulli
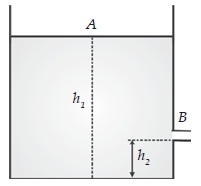 Skema persamaan Bernoulli untuk fluida dalam tangki dan terdapat kebocoran dalam ketinggian tertentu.
Skema persamaan Bernoulli untuk fluida dalam tangki dan terdapat kebocoran dalam ketinggian tertentu.
contoh soal:
Tangki air dengan lubang kebocoran diperlihatkan gambar berikut!

Jarak lubang ke tanah adalah 10 m dan jarak lubang ke permukaan air adalah 3,2 m. Tentukan:
a) Kecepatan keluarnya air
b) Jarak mendatar terjauh yang dicapai air
c) Waktu yang diperlukan bocoran air untuk menyentuh tanah
Pembahasan
a) Kecepatan keluarnya air
v = √(2gh)
v = √(2 x 10 x 3,2) = 8 m/s
b) Jarak mendatar terjauh yang dicapai air
X = 2√(hH)
X = 2√(3,2 x 10) = 8√2 m
c) Waktu yang diperlukan bocoran air untuk menyentuh tanah
t = √(2H/g)
t = √(2(10)/(10)) = √2 sekon

untuk menentukan kelajuan fluida pada penampang diperoleh:
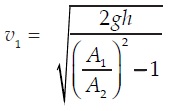
contoh soal:

diperoleh :
gh%7D%7B%5Crho+%5Cleft+(+A_%7B1%7D%5E%7B2%7D-A_%7B2%7D%5E%7B2%7D+%5Cright+)%7D%7D)


diperoleh rumus:
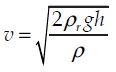


contoh soal:
Gaya angkat yang terjadi pada sebuah pesawat diketahui sebesar 1100 kN.

Pesawat tersebut memiliki luas penampang sayap sebesar 80 m2. Jika kecepatan aliran udara di bawah sayap adalah 250 m/s dan massa jenis udara luar adalah 1,0 kg/m3 tentukan kecepatan aliran udara di bagian atas sayap pesawat!
Pembahasan
Data soal:
A = 80 m2
νb = 250 m/s
ρ = 1,0 kg/m3
F = 1100 kN = 1100 000 N
νa =......

latihan latihan soal:
1. Tentukan besar debit dari suatu aliran air yang melalui sebuah pipa berdiameter 4 cm dengan kecepatan rata-rata 4 m/s
2.Pada sebuah sungai bawah tanah air mengalir dari hulu ke hilir. Kita anggap sungai berbentuk lingkaran dengan diameter bagian hulu sebesar 6 m dan bagian hilir 10 m. Jika kelajuan aliran air pada sungai bagian hulu sebesar 10 m/s, maka hitunglah kelajuan aliran air pada sungai bagian hilir!
sampai disini saja .semoga bermanfaat..
3. Tentukan kecepatan aliran udara di bagian atas sayap, jika kecepatan aliran udara di bagian bawah sayap pesawat adalah 60 m/s dan beda tekanan di atas dan di bawah sayap adalah 10 N/m2 (ρudara = 1,29 kg/m3


guru indri dayana,M.Si
tujuan pembelajaran:mengetahui konsep fluida iddeal,garis arus dan asas kontinuitas,asas bernoulli dan mengetahui pnerapan penerapan asas kontinuitas dan asas bernoulli dalam kehidupan serta dapat mengerjakan latihan latiahn fluida dinami
apakah yang dimaksud dengan fluida dinamis? fluida dinamis adalah fluida yang bergerak.
beberapa konsep tentang fluida dinamis:
1.fluida termampatkan :fluida yang volume atau massa jenisnya berubah ketika diberi tekanan
2.fluida tak termampatkan :fluida yang volume atau massa jenisnya tetap ketika diberi tekanan
3.aliran tunak : aliran fluida dimana kecepatan fluida di setiap titik adalah tetap.
4.aliran tidak tunak: aliran fluida dimana kecepatan fluida di setiap titik tidak tetap
5.aliran berputar: fluida tersebut mengalami momentum sudut terhadap suatu titik tertentu
6. aliran tidak berputar: fluida tersebut tidak mengalami momentum sudut terhadap suatu titik tertentu
7. fluida kental: fluida dimana gesekan internal di dalam fluida tidak dapat diabaikan sehingga benda bergerak melalui fluida tersebut mengalami gaya gesekan
8.fluida tak kental :fluida dimana gesekan internal di dalam fluida dapat diabaikan sehingga benda bergerak melalui fluida tersebut tidakmengalami gaya gesekan
garis arus dan asas kontinuitas
1. garis arus
adalah lintasan yang ditempuh oleh partikel-partikel fluida yang mengalir dengan aliran tunak.
2.asas kontinuitas
sebelum mempelajari asas kontinuitas terlebih dahulu memahami konsep debit
debit adalah besaran fisis yang menyatakan volume fluida yang mengalir melalui suatu penampang tiap satuan waktu.
Debit
keterangan :
Q = debit (m3/s)
V = volume (m3)
t = waktu (s)
Q = debit (m3/s)
V = volume (m3)
t = waktu (s)
jd persamaan kontinuitas adalah Persamaan kontinuitas adalah persamaan yang menghubungkan kecepatan fluida dalam dari satu tempat ke tempat lain
menurut asas kontinuitas "untuk fluida tak termampatkan hasil kali antara luas penampang dengan besar kecepatan fluida selalu tetap" karena hasil kali antara luas penampang dengan kecepatan adalah debit aliran fluida maka pernyataan lain dari asas kontinuitas adalah "untuk fluida tak termampatkan,debit aliran fluida di setiap titik adalah tetap."
contoh soal:
Pipa saluran air bawah tanah memiliki bentuk seperti gambar berikut!

Jika luas penampang pipa besar adalah 5 m2 , luas penampang pipa kecil adalah 2 m2 dan kecepatan aliran air pada pipa besar adalah 15 m/s, tentukan kecepatan air saat mengalir pada pipa kecil!
Pembahasan
Persamaan kontinuitas
A1v1 = A2v2
(5)(15) = (2) v2
v2 = 37,5 m/s
C. asas bernouli
Hukum Bernoulli adalah hukum yang berlandaskan pada hukum kekekalan energi yang dialami oleh aliran fluida. Hukum ini menyatakan bahwa jumlah tekanan

persamaan ini mempunyai makna fifis yaitu "untuk fluida ideal yang mengalir melalui suatu penampang,jumlah tekanan,energi potensial per satuan dari fluida tersebut di setiap titik sepanjang garis arus bernilai konstan"
D.penerapan asas kontinuitas dan asas bernoulli
- pada tangki yang berlubang
 Skema persamaan Bernoulli untuk fluida dalam tangki dan terdapat kebocoran dalam ketinggian tertentu.
Skema persamaan Bernoulli untuk fluida dalam tangki dan terdapat kebocoran dalam ketinggian tertentu.
Perhatikan gambar diatas, pada titik A, kecepatan fluida turun relatif kecil sehingga dianggap nol (v1 = 0). Oleh karena itu persamaan Bernoulli menjadi sebagai berikut.
p1 + ρgh1 + 0 = p2 +ρgh2 +  ρv22
ρv22
g(h1 – h2) =  v2
v2
v = %7D)
Jika h1–h2 = h, maka:
v = 
Perhatikan gambar diatas. Jika air keluar dari lubang B dengan kelajuan v yang jatuh di titik D, maka terlihat lintasan air dari titik B ke titik D berbentuk parabola. Berdasarkan analisis gerak parabola, kecepatan awal fluida pada arah mendatar sebesar vBX = v =  . Sedangkan kecepatan awal pada saat jatuh (sumbu Y) merupakan gerak lurus berubah beraturan (GLBB) dengan percepatan ay = g. Berdasarkan persamaan jarak Y = v0yt +
. Sedangkan kecepatan awal pada saat jatuh (sumbu Y) merupakan gerak lurus berubah beraturan (GLBB) dengan percepatan ay = g. Berdasarkan persamaan jarak Y = v0yt +  ay t2 dengan Y = H –h, v0y = 0, dan ay = g, maka kita peroleh persamaan untuk menghitung waktu yang diperlukan air dari titik B ke titik D sebagai berikut.
ay t2 dengan Y = H –h, v0y = 0, dan ay = g, maka kita peroleh persamaan untuk menghitung waktu yang diperlukan air dari titik B ke titik D sebagai berikut.
X = v0X t
Karena v0X = vBX = v =  , maka:
, maka:
R = X = 
%7D%7Bg%7D%7D)
R = X = %7D)
R = X = %7D)
contoh soal:
Tangki air dengan lubang kebocoran diperlihatkan gambar berikut!

Jarak lubang ke tanah adalah 10 m dan jarak lubang ke permukaan air adalah 3,2 m. Tentukan:
a) Kecepatan keluarnya air
b) Jarak mendatar terjauh yang dicapai air
c) Waktu yang diperlukan bocoran air untuk menyentuh tanah
Pembahasan
a) Kecepatan keluarnya air
v = √(2gh)
v = √(2 x 10 x 3,2) = 8 m/s
b) Jarak mendatar terjauh yang dicapai air
X = 2√(hH)
X = 2√(3,2 x 10) = 8√2 m
c) Waktu yang diperlukan bocoran air untuk menyentuh tanah
t = √(2H/g)
t = √(2(10)/(10)) = √2 sekon
- venturimeter
merupakan alat yang digunakan untuk mengukur kelajuan aliran suatu fluida/zat cair
venturimeter tanpa manometer

untuk menentukan kelajuan fluida pada penampang diperoleh:
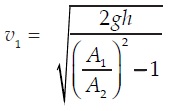
contoh soal:
Untuk mengukur kecepatan aliran air pada sebuah pipa horizontal digunakan alat seperti diperlihatkan gambar berikut ini!

Jika luas penampang pipa besar adalah 5 cm2 dan luas penampang pipa kecil adalah 3 cm2 serta perbedaan ketinggian air pada dua pipa vertikal adalah 20 cm tentukan :
a) kecepatan air saat mengalir pada pipa besar
b) kecepatan air saat mengalir pada pipa kecil
Pembahasan
Rumus kecepatan fluida memasuki pipa venturimetar pada soal di atas

Jika luas penampang pipa besar adalah 5 cm2 dan luas penampang pipa kecil adalah 3 cm2 serta perbedaan ketinggian air pada dua pipa vertikal adalah 20 cm tentukan :
a) kecepatan air saat mengalir pada pipa besar
b) kecepatan air saat mengalir pada pipa kecil
Pembahasan
Rumus kecepatan fluida memasuki pipa venturimetar pada soal di atas
v1 = A2√ [(2gh) : (A12 − A22) ]
a) kecepatan air saat mengalir pada pipa besar
v1 = A2√ [(2gh) : (A12 − A22) ]
v1 = (3) √ [ (2 x 10 x 0,2) : (52 − 32) ]
v1 = 3 √ [ (4) : (16) ]
v1 = 1,5 m/s
v1 = A2√ [(2gh) : (A12 − A22) ]
v1 = (3) √ [ (2 x 10 x 0,2) : (52 − 32) ]
v1 = 3 √ [ (4) : (16) ]
v1 = 1,5 m/s
- venturimeter dengan manometer

diperoleh :

- karburator
alat pada mesin yang digunakan unruk menghasilkan campuran bahan bakar dengan udara pada proses pembakaran dalam mesin
- penyemprot nyamuk
memiliki prinsip kerja yang mirip dengan karburator.ketika pengisap pompa ditekan,udara dari tabung silinder dipaksa keluar melalui lubang sempit.udara yang keluar dari lubang sempit ini mempunyai kecepatan tinggi sehingga menurunkan tekanan udara di bagian atas nosel.
- tabung pilot
merupakan alat yang digunakan untuk mengukur laju aliran gas atau udara.

diperoleh rumus:
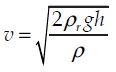
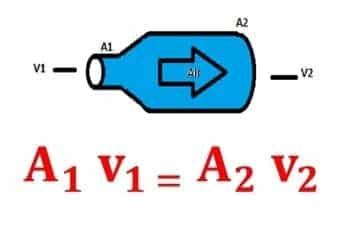
- pada sayap pada pesawat terbang
Penampang sayap pesawat terbang mempunyai bagian belakang yang lebih tajam dan sisi bagian atas yang lebih melengkung daripada sisi bagian bawahnya. Perhatikan gambar dibawah. Garis arus pada sisi bagian atas lebih rapat daripada sisi bagian bawahnya. Artinya, kelajuan aliran udara pada sisi bagian atas pesawat v2 lebih besar daripada sisi bagian bawah sayap v1. Sesuai dengan asas Bornoulli, tekanan pada sisi bagian atas p2 lebih kecil daripada sisi bagian bawah p1 karena kelajuan udaranya lebih besar. Dengan A sebagai luas penampang pesawat, maka besarnya gaya angkat dapat kita ketahui melalui persamaan berikut.


contoh soal:
Gaya angkat yang terjadi pada sebuah pesawat diketahui sebesar 1100 kN.

Pesawat tersebut memiliki luas penampang sayap sebesar 80 m2. Jika kecepatan aliran udara di bawah sayap adalah 250 m/s dan massa jenis udara luar adalah 1,0 kg/m3 tentukan kecepatan aliran udara di bagian atas sayap pesawat!
Pembahasan
Data soal:
A = 80 m2
νb = 250 m/s
ρ = 1,0 kg/m3
F = 1100 kN = 1100 000 N
νa =......

latihan latihan soal:
1. Tentukan besar debit dari suatu aliran air yang melalui sebuah pipa berdiameter 4 cm dengan kecepatan rata-rata 4 m/s
2.Pada sebuah sungai bawah tanah air mengalir dari hulu ke hilir. Kita anggap sungai berbentuk lingkaran dengan diameter bagian hulu sebesar 6 m dan bagian hilir 10 m. Jika kelajuan aliran air pada sungai bagian hulu sebesar 10 m/s, maka hitunglah kelajuan aliran air pada sungai bagian hilir!
sampai disini saja .semoga bermanfaat..
3. Tentukan kecepatan aliran udara di bagian atas sayap, jika kecepatan aliran udara di bagian bawah sayap pesawat adalah 60 m/s dan beda tekanan di atas dan di bawah sayap adalah 10 N/m2 (ρudara = 1,29 kg/m3
4. Sebuah tangki air memiliki lubang kebocoran. Jarak lubang ke tanah adalah 10 m dan jarak lubang ke permukaan air adalah 3,2 m. Tentukan:
a) Kecepatan keluarnya air
b) Jarak mendatar terjauh yang dicapai air
c) Waktu yang diperlukan bocoran air untuk menyentuh tanah
berikut adalah pembahasannya
1.Diketahui: d = 4 cm = 4 × 10–2 m r = 2 × 10–2 m v = 4 m/s
Ditanyakan: debit (Q)
A = luas lingkaran
A = π r2 = 3,14 × (2 × 10-2)2 = 1,256 × 10-3 m2
Q = A v = 1,256 × 10-3 × 4 = 5,024 × 10-3 m2 /s
2
3.
4 a) Kecepatan keluarnya air
v = √(2gh)
v = √(2 x 10 x 3,2) = 8 m/s
b) Jarak mendatar terjauh yang dicapai air
v = √(2gh)
v = √(2 x 10 x 3,2) = 8 m/s
b) Jarak mendatar terjauh yang dicapai air
X = 2√(hH)
X = 2√(3,2 x 10) = 8√2 m
c) Waktu yang diperlukan bocoran air untuk menyentuh tanah
t = √(2H/g)
t = √(2(10)/(10)) = √2 sekon
X = 2√(3,2 x 10) = 8√2 m
c) Waktu yang diperlukan bocoran air untuk menyentuh tanah
t = √(2H/g)
t = √(2(10)/(10)) = √2 sekon


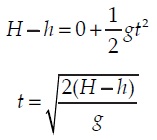

Komentar
Posting Komentar