Dinamika rotasi dan keseimbangan benda tegar
tugas proyek fisika kelas XI semester ganjil
guru indri dayana,M.Si
materi pembelajaran :dinamika rotasi dan keseimbangan benda tegar
tujuan pembelajaran: mengetahui apa yang dimaksud dengan benda tegar,definisi dari momen gaya,kopel,inersia,serta mngetahui jenis jenis keseimbangan ,dan dapat mengerjakan soal soal dinamika rotasi dan keseimbangan benda tegar
apa yang dimaksud dengan benda tegar?benda tegar didefinisikan sebagai benda yang tidak mengalami perubahan bentuk ketika suatu gaya dikerjakan padanya.
1. momen gaya
definisi: sebagai hasil perkalian silang antara vektor posisi titik kerja gaya terhadap poros dengan vektor gaya
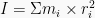

M = momen kopel (N . m)
L = lengan gaya (m)
F = gaya (N)
α = sudut antara lengan gaya dan gaya
a. Macam momen kopel ada dua, yaitu kopel positif dan kopel negatif.
3. momen inersia
definisi: sebuah partikel yang berotasi pada porosnya didefinisikan sebagai hasil kali massa partikel dengan kuadrat jarak partikel terhadap sumbu putarnya atau porosnya
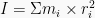

4. momentum sudut
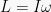
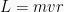


guru indri dayana,M.Si
materi pembelajaran :dinamika rotasi dan keseimbangan benda tegar
tujuan pembelajaran: mengetahui apa yang dimaksud dengan benda tegar,definisi dari momen gaya,kopel,inersia,serta mngetahui jenis jenis keseimbangan ,dan dapat mengerjakan soal soal dinamika rotasi dan keseimbangan benda tegar
apa yang dimaksud dengan benda tegar?benda tegar didefinisikan sebagai benda yang tidak mengalami perubahan bentuk ketika suatu gaya dikerjakan padanya.
1. momen gaya
definisi: sebagai hasil perkalian silang antara vektor posisi titik kerja gaya terhadap poros dengan vektor gaya
Torsi atau momen gaya
Satuan dari torsi adalah Nm (Newton meter).
2. momen kopel
definisi: pasangan 2 buah gaya yang sama besar, mempunyai garis kerja yang sejajar dan arahnya berlawanan.
M = momen kopel (N . m)
L = lengan gaya (m)
F = gaya (N)
α = sudut antara lengan gaya dan gaya
a. Macam momen kopel ada dua, yaitu kopel positif dan kopel negatif.
3. momen inersia
definisi: sebuah partikel yang berotasi pada porosnya didefinisikan sebagai hasil kali massa partikel dengan kuadrat jarak partikel terhadap sumbu putarnya atau porosnya
I adalah momen inersia (kgm2)
r adalah jari-jari (m)
m adalah massa benda atau partikel (kg)
m adalah massa benda atau partikel (kg)
| Benda | Poros | Gambar | Momen inersia |
|---|---|---|---|
| Batang silinder | Poros melalui pusat |  | |
| Batang silinder | poros melalui ujung |  | |
| Silinder berongga | Melalui sumbu |  | |
| Silinder pejal | Melalui sumbu | 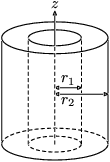 | |
| Silinder pejal | Melintang sumbu |  | |
| Bola pejal | Melalui diameter |  | |
| Bola pejal | Melalui salahsatu garis singgung |  | |
| Bola berongga | Melalui diameter |  |
definisi : sebagai vektor hasil momen inersia dengan kecepatan sudut.
dimana:
L adalah momentum sudut (kgm2s-1)
I adalah momen inersia benda (kgm2)
 adalah kecepatan sudut benda (rad/s)
adalah kecepatan sudut benda (rad/s)
m adalah massa benda (kg)
v adalah kecepatan linear (m/s)
r adalah jarak benda ke sumbu putarnya (m)
L adalah momentum sudut (kgm2s-1)
I adalah momen inersia benda (kgm2)
m adalah massa benda (kg)
v adalah kecepatan linear (m/s)
r adalah jarak benda ke sumbu putarnya (m)
Hubungan antara torsi dengan momen inersia
Hukum II Newton tentang rotasi
Keterangan:
- I : momen inersia (kg m²)
- α : percepatan sudut (rad/s²)
- : torsi (Nm)
5. energi dan usaha pada gerak rotasi
a. energi kinetik rotasi
b usaha dalam gerak rotasi
W = τ . θ
dengan:
W = usaha ( J)
τ = momen gaya (Nm2)
θ = sudut yang ditempuh
Usaha yang dilakukan oleh momen gaya sama dengan perubahan energi kinetik rotasi:
W = Δ Ekrot = ½ I. ω22 – I. ω12
c gabungan energi kinetik translasi dan rotasi
d. Energi total atau energi mekanik dirumuskan:
keseimbangan benda tegar
adalah kondisi dimana momentum benda tegar sama dengan nol. Artinya jika awalnya benda tegar tersebut diam, maka ia akan tetap diam. Namun jika awalnya benda tegar tersebut bergerak dengan kecepatan konstan, maka ia akan tetap bergerak dengan kecepatan konstan.
1. keseimbangan partikel
Sebuah partikel atau benda titik dikatakan seimbang jika resultan gaya-gaya yang bekerja padanya sama dengan nol.
Σ F = 0
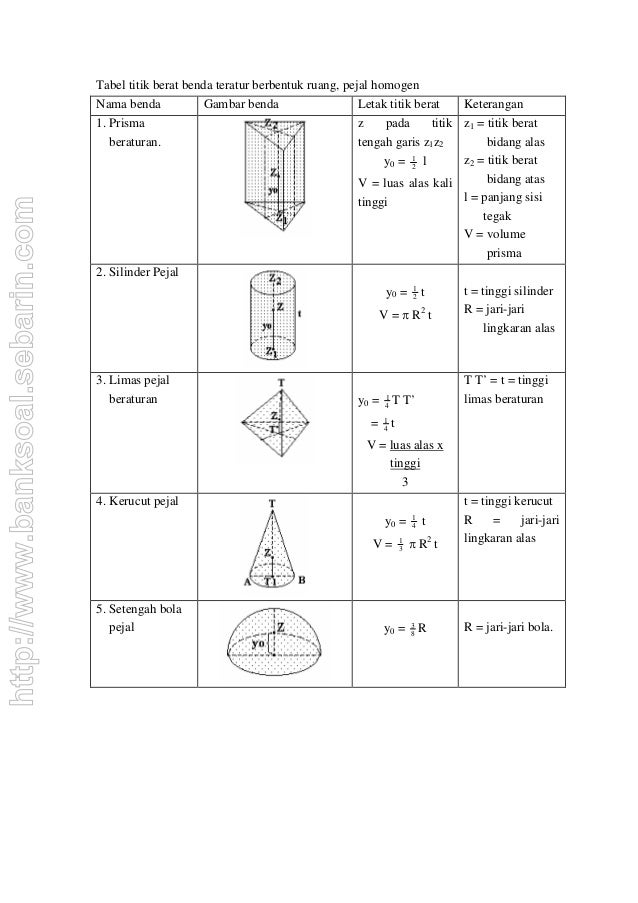
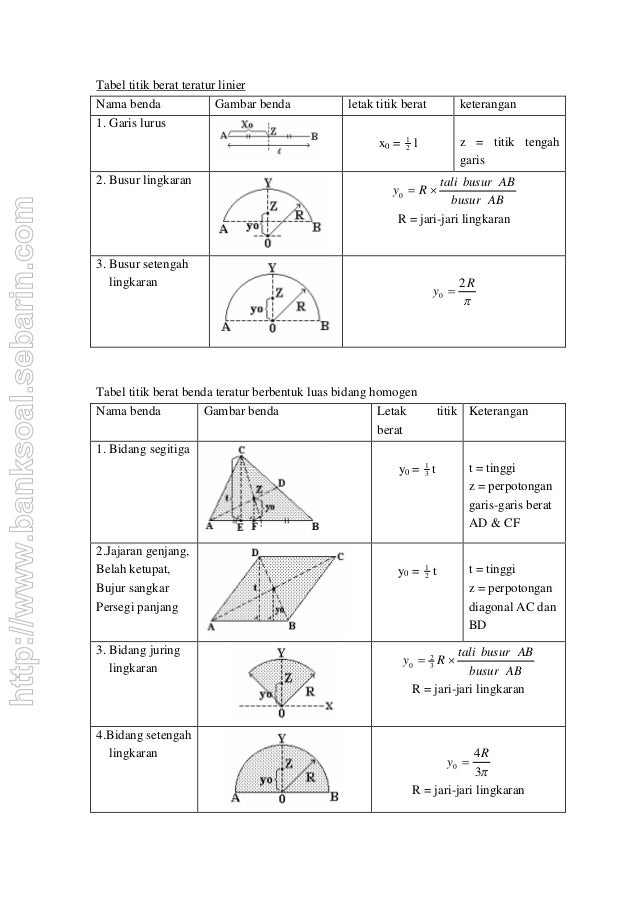
2. titik berat dan titik pusat massa
titik pusat massa adalah titik yang mewakili posisi benda bila dianggap sebagai suatu titik partikel.
titik berat tidak sama dengan titik pusat massa meskipun pada umumnya titik berat suatu benda berimpit dengan titik pusat massanya.



jenis jenis keseimbangan:
1. keseimbangan stabil atau keseimbangan mantap adalah keseimbangan yang dialami benda dimana benda akan kembali ke kedudukan seimbangnya semula setelah gangguan pada benda tersebut dihilangkan.
2. keseimbangan labil adalah keseimbangan yang dialami benda dimana benda tidak akan kembali ke kedudukan seimbangnya semula setelah gangguannya dihilangkan,tetapi justru meningkatkan gangguan tersebut
3. keseimbangan netral atau keseimbangan indiferen adalah keseimbangan yang dialami benda dimana gangguan kecil yang diberikan pada benda tidak memengaruhi kedudukan keseimbangan benda.
berikut adalah contoh soalnya:
 Percepatan kedua benda dihitung menggunakan rumus hukum II Newton.
Percepatan kedua benda dihitung menggunakan rumus hukum II Newton.
∑F = m a
wB –T+T-T+T-fges = (mA + mB) a
10 – 2,5 = (2 + 1) a
7,5 = 3a
a = 2,5 m/s2
1. keseimbangan stabil atau keseimbangan mantap adalah keseimbangan yang dialami benda dimana benda akan kembali ke kedudukan seimbangnya semula setelah gangguan pada benda tersebut dihilangkan.
2. keseimbangan labil adalah keseimbangan yang dialami benda dimana benda tidak akan kembali ke kedudukan seimbangnya semula setelah gangguannya dihilangkan,tetapi justru meningkatkan gangguan tersebut
3. keseimbangan netral atau keseimbangan indiferen adalah keseimbangan yang dialami benda dimana gangguan kecil yang diberikan pada benda tidak memengaruhi kedudukan keseimbangan benda.
berikut adalah contoh soalnya:
1. Dari gambar berikut, balok A mempunyai massa 2 kg dan balok B = 1Kg. bila gaya gesekan antara benda A dengan bidang 2,5 Newton, sedangkan gaya gesekan tali dengan katrol diabaikan, maka percepatan kedua benda adalah..
A. 20,0 m.s-2
C. 6,7 m.s-2
D. 3,3 m.s-2
E. 2,5 m.s-2
Jawaban: E
Pembahasan :
Jawab :
∑F = m a
wB –T+T-T+T-fges = (mA + mB) a
10 – 2,5 = (2 + 1) a
a = 2,5 m/s2
2. Dua buah bola yang dihubungkan dengan kawat (massa kawat diabaikan) disusun seperti gambar. Besar momen inersianya adalah…
B. 25 x 10-3 kg.m2
C. 11 x 10-2 kg.m2
D. 55 x 10-2 kg.m2
E. 80 x 10-2 kg.m2
Jawaban: B
Pembahasan :
Diketahui : Massa bola A (mA) = 200 gram = 0,2 kg
Massa bola B (mB) = 400 gram = 0,4 kg
Jarak antara bola A dan sumbu rotasi (rA) = 0
Jarak antara bola B dan sumbu rotasi (rB) = 25 cm = 0,25 meter
Jarak antara bola A dan sumbu rotasi (rA) = 0
Jarak antara bola B dan sumbu rotasi (rB) = 25 cm = 0,25 meter
Ditanya : Momen inersia (I) sistem=?
Jawab :
Jawab :
· Momen inersia bola A
IA = (mA)(rA2) = (0,2)(0)2 = 0
IA = (mA)(rA2) = (0,2)(0)2 = 0
· Momen inersia bola B
IB = (mB)(rB2) = (0,4)(0,25)2 = (0,4)(0,0625) = 0,025 kg m2
IB = (mB)(rB2) = (0,4)(0,25)2 = (0,4)(0,0625) = 0,025 kg m2
Momen inersia sistem partikel :
I = IA + IB = 0 + 0,025 = 0,025 kg m2 = 25 x 10-3 kg m2
I = IA + IB = 0 + 0,025 = 0,025 kg m2 = 25 x 10-3 kg m2
3. Sebuah batang yang diabaikan massanya dipengaruhi tiga buah gaya FA = FC = 10 N dan FB = 20 N seperti gambar. Jika jarak AB = BC = 20 cm, maka besar momen gaya terhadap titik C adalah…
B. 1 Nm
C. 4 Nm
D. 6 Nm
E. 8 Nm
Jawaban : A
Pembahasan :
Diketahui : Sumbu rotasi terletak di titik C.
Jarak antara FA dan sumbu rotasi (rAC) = 40 cm = 0,4 meter
Jarak antara FB dan sumbu rotasi (rBC) = 20 cm = 0,2 meter
Jarak antara FC dan sumbu rotasi (rCC) = 0 cm
FA = 10 Newton
FB = 20 Newton
FC = 10 Newton
Jarak antara FB dan sumbu rotasi (rBC) = 20 cm = 0,2 meter
Jarak antara FC dan sumbu rotasi (rCC) = 0 cm
FA = 10 Newton
FB = 20 Newton
FC = 10 Newton
Ditanya : Resultan momen gaya jika batang diputar pada poros di C=?
Jawab :
Jawab :
momen gaya yang ditimbulkan oleh masing-masing gaya.
Resultan momen gaya
4. Sebuah bola pejal bermassa 0,25 kg dan jari-jari 20 cm berotasi dengan kecepatan sudut 20 rad/s. Berapakah momentum sudut bola tersebut?
Penyelesaian
m = 0,5 kg, R = 0,2 m, ω = 15 rad
bola pejal : k = 2/5
Momentum sudut bola sebesar :
L = I ω
= (2/5) mR2. ω
= (2/5).(0,25).(0,2)2. 20
= 0,8 kg m2/s
5. Silinder pejal berjari-jari 8 cm dan massa 2 kg. Sedangkan bola pejal berjari-jari 5 cm dan massa 4 kg. Jika kedua benda tadi berotasi dengan poros melalui pusatnya maka tentukan perbandingan momen inersia silinder dan bola!
Penyelesaian
mS = 2 kg, RS = 8 cm = 8.10-2 m
mB = 4 kg, RB = 5 cm = 5.10-2 m
Momen inersia silinder pejal :
IS = ½ mS RS2
= ½ . 2. (8.10-2)2 = 64.10-4 kg m2
Momen inersia bola pejal :
IB = mB RB2
= 2/5 . 4. (5.10-2)2 = 40.10-4 kg m2
Perbandingannya sebesar :
IS : IB
64.10-4 : 40.10-4
8 : 5
nah berikut adalah soal soal latihan:
1.Sebuah batang yang sangat ringan, panjangnya 140 cm. Pada batang bekerja tiga gaya masing-masing F1 = 20 N, F2 = 10 N, dan F3 = 40 N dengan arah dan posisi seperti pada gambar. Besar momen gaya yang menyebabkan batang berotasi pada pusat massanya adalah …
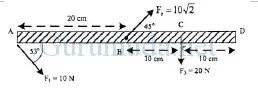
2.Batang AB yang massanya diabaikan diletakkan mendatar dan dikerjakan tiga buah gaya seperti gambar. Resultan momen gaya yang bekerja pada batang jika diputar pada poros di D adalah… (sin 53o = 0,8)

3.Perhatikan gambar dua bola yang dihubungkan dengan seutas kawat. Panjang kawat = 12 m, l1 = 4 m dan massa kawat diabaikan, maka besarnya momen inersia sistem adalah…
4.Sebuah katrol cakram pejal massanya 8 kg dan berjari-jari 10 cm pada tepinya dililitkan seutas tali yang ujungnya diikatkan beban 4 kg (g = 10 ms-2 ). Percepatan gerak turunnya beban adalah


















Komentar
Posting Komentar